Message Passing Transformers

This post shows a graph (“message passing” or “soft dictionary lookup”) interpretation of Attention. It combines two really great references on the topic that show that forward passes through transformers are similar to message passing algorithms for probabilistic graphical models. But instead of the NP-hardness of the Belief Propagation algorithm, transformers scale as $O(n^2 * d)$ with the data.

Attention as soft dictionary lookup

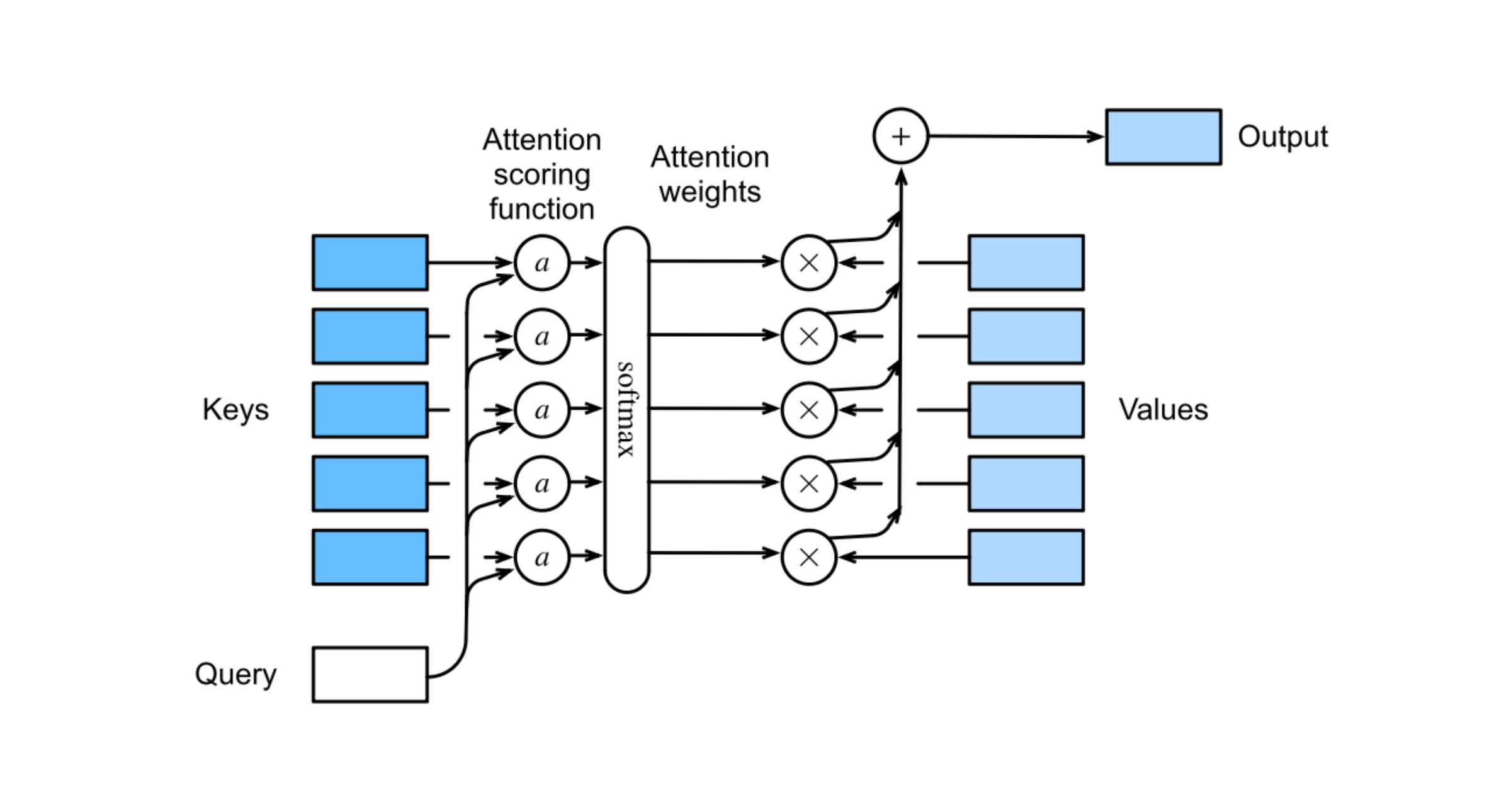
This was inspired from Section 15.4.1 of Kevin Murphy’s Probabilistic Machine Learning (PML) textbook. Attention operation accepts a query (from a node) and a set of (key, value) tuples (from all other nodes):

\[\text{Attn}(\pmb q, (\pmb k_1, \pmb v_1), \dots, (\pmb k_m, \pmb v_m)) = \text{Attn}(\pmb q, (\pmb k_{1:m}, \pmb v_{1:m})) = \sum_{i=1}^m \alpha_i (\pmb q, \pmb k_{1:m})\pmb v_i \in \mathbb R^v\]

The attention weights $\alpha_i$:

\[\alpha_i(\pmb q, \pmb k_{1:m}) = \text{softmax}_i([a(\pmb q, \pmb k_1), \dots, a(\pmb q, \pmb k_m)]) = \frac{\exp{a(\pmb q, \pmb k_i)}}{\sum_{j=1}^m \exp{a(\pmb q, \pmb k_j)}}\]

have the properties:

\[0 \leq \alpha_i(\pmb q, \pmb k_{1:m}) \leq 1\] \[\sum_i \alpha_i(\pmb q, \pmb k_{1:m}) = 1\]

For attention score $a$ which computes the similarity between $\pmb q$ and $\pmb k_i$:

\[a: \pmb q \times \pmb k_i \rightarrow \mathbb R\]

Finally, the computation graph can be visualized as (credit to Dive into Deep Learning):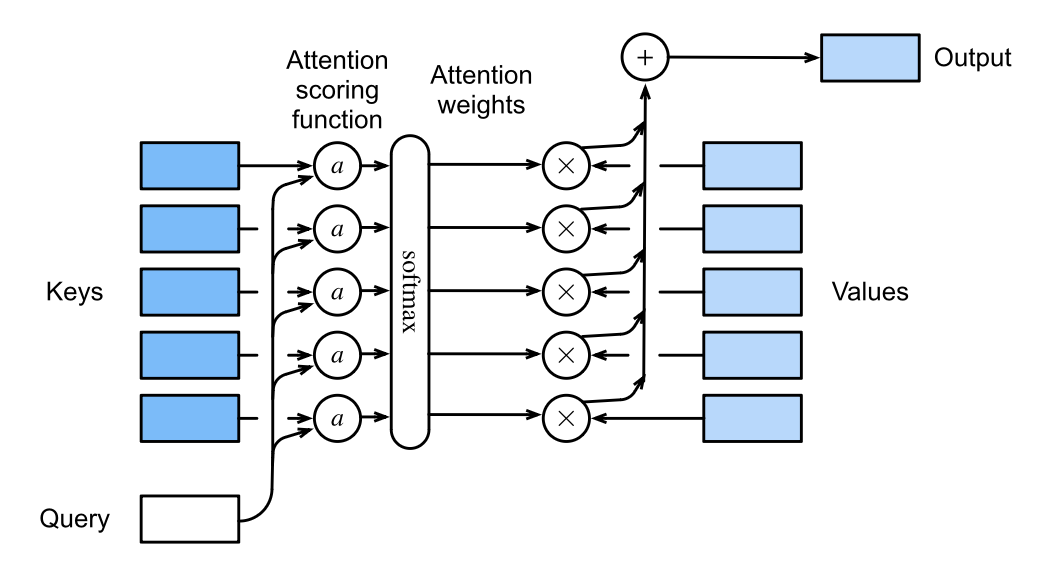

Message Passing (Python)

This python code directly taken from Andrej Karpathy’s lecture on Transformers. The idea is to represent each data point (embeddings of tokens in a sequence) as a node in a graph and then connect them (fully or casually). Instead of dealing with this data directly, we project the data into the query, key, and value data. This improves the representation of the underlying data. The algorithm finally updates itself by taking a convex combination of the values with attention scores (i.e. the attention weights).

import numpy as np
import networkx as nx
from pprint import pprint

Implementation

class Node:
    def __init__(self):
        self.data = np.random.randn(20)
        self.wkey = np.random.randn(20, 20)
        self.wquery = np.random.randn(20, 20)
        self.wvalue = np.random.randn(20, 20)

    def key(self):
        # what do I have
        return self.wkey @ self.data

    def query(self):
        # what am I looking for?
        return self.wquery @ self.data

    def value(self):
        # what do I publicly reveal/broadcast to others?
        return self.wvalue @ self.data

class Graph:
    def __init__(self):
        self.nodes = [Node() for i in range(10)]
        randi = lambda: np.random.randint(len(self.nodes))
        self.edges = [(randi(), randi()) for _ in range(40)]
        # dedup edges
        self.edges = list(set(list(self.edges)))

    def run_node(self, i: int, n: Node) -> np.ndarray:
        print(f"++++ ito: {i}")
        # each node has one question
        q = n.query()
        ifroms = [ifrom for (ifrom, ito) in self.edges if ito == i]
        inputs = [self.nodes[ifrom] for ifrom in ifroms]
        print(f"\tifroms: {ifroms}")

        # each key from all connected nodes
        keys = [m.key() for m in inputs]
        scores = [k.dot(q) for k in keys]
        print(f"\tscores: {scores}")
        scores = np.exp(scores)
        scores = scores / np.sum(scores)
        print(f"\tAttention weights: {scores}")
        print(f"\tsum_i scores_i = {sum(scores)}")

        # each value from all connected nodes
        values = [m.value() for m in inputs]
        # each vector is (20,)
        updates = [s * v for s, v in zip(scores, values, strict=True)]
        # resulting update is (20,)
        update = np.array(updates).sum(axis=0)
        print()
        return update

    def run(self):
        updates = []
        for i, n in enumerate(self.nodes):
            update = self.run_node(i=i, n=n)
            updates.append(update)

        # add all
        for n, u in zip(self.nodes, updates, strict=True):
            n.data = n.data + u

Results

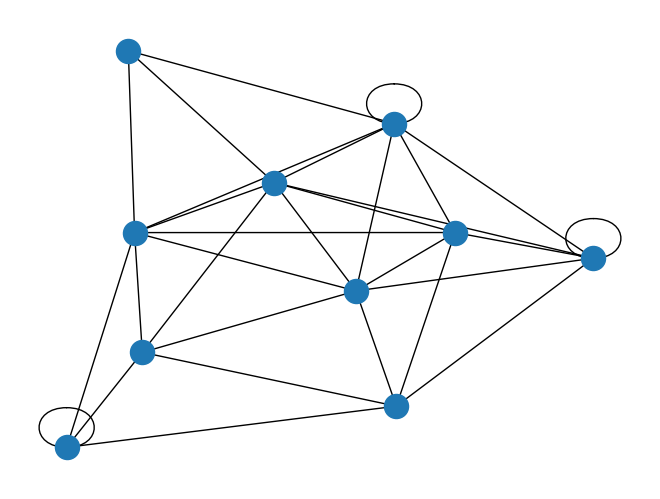
graph = Graph()
G = nx.from_edgelist(graph.edges)
print(G)
print()
print("Nodes")
print(G.nodes)
print()
print("Edge List")
pprint({k: list(dict(v).keys()) for k, v in G.adj.items()})

Graph with 10 nodes and 30 edges

Nodes
[4, 0, 3, 9, 7, 6, 5, 8, 1, 2]

Edge List
{0: [4, 8, 3, 7, 6],
 1: [6, 9, 2, 5, 8, 1, 4],
 2: [5, 8, 4, 1, 6, 7],
 3: [4, 7, 0, 3],
 4: [0, 3, 9, 6, 2, 8, 1],
 5: [7, 2, 6, 8, 1, 5],
 6: [4, 8, 1, 5, 0, 2, 9],
 7: [3, 5, 0, 8, 2],
 8: [6, 0, 2, 4, 5, 1, 7],
 9: [4, 1, 6]}

nx.draw(G)

graph.run()

++++ ito: 0
	ifroms: [4, 3, 7, 6]
	scores: [66.28713441407328, -42.356895194685464, -72.42356412336589, 37.33998459065121]
	Attention weights: [1.00000000e+00 6.55386436e-48 5.73731961e-61 2.68171465e-13]
	sum_i scores_i = 0.9999999999999999

++++ ito: 1
	ifroms: [9, 1]
	scores: [211.47668629424436, 77.85702511746038]
	Attention weights: [1.00000000e+00 9.32649533e-59]
	sum_i scores_i = 1.0

++++ ito: 2
	ifroms: [4, 1, 7]
	scores: [35.58941250531445, -53.70434487821338, -80.78903024029921]
	Attention weights: [1.00000000e+00 1.66040449e-39 2.86737506e-51]
	sum_i scores_i = 1.0

++++ ito: 3
	ifroms: [4, 3, 7]
	scores: [31.240260256884994, 5.379888043038299, 59.36660338598627]
	Attention weights: [6.09374649e-13 3.57987144e-24 1.00000000e+00]
	sum_i scores_i = 1.0

++++ ito: 4
	ifroms: [0, 8, 1]
	scores: [-23.23660787608064, 34.19954420654749, -74.67617928930356]
	Attention weights: [1.13709327e-25 1.00000000e+00 5.19845241e-48]
	sum_i scores_i = 1.0

++++ ito: 5
	ifroms: [2, 8, 1, 5]
	scores: [-79.00370928667077, 19.908000741887548, -75.48698208523935, -44.17319414548691]
	Attention weights: [1.10456210e-43 1.00000000e+00 3.71950680e-42 1.47873607e-28]
	sum_i scores_i = 1.0

++++ ito: 6
	ifroms: [4, 8, 1, 5, 0, 2]
	scores: [-23.987304007919384, 8.42476207930093, -84.15587488072015, 69.30330615398142, -287.98108781017044, -11.46404257694845]
	Attention weights: [3.05072312e-041 3.63734288e-027 2.25696321e-067 1.00000000e+000
 6.81332697e-156 8.37888304e-036]
	sum_i scores_i = 1.0

++++ ito: 7
	ifroms: [3, 5, 8]
	scores: [-23.8989411122908, -6.459026663244714, 13.084969606201714]
	Attention weights: [8.67144860e-17 3.25199796e-09 9.99999997e-01]
	sum_i scores_i = 1.0

++++ ito: 8
	ifroms: [0, 2, 6, 4, 1, 7]
	scores: [-44.044223084610195, 18.67462267889491, 71.68866337449023, -32.61671246043159, -52.38386938730109, -27.39714905660486]
	Attention weights: [5.46822072e-51 9.46879387e-24 1.00000000e+00 5.02054475e-46
 1.30612176e-54 9.28065068e-44]
	sum_i scores_i = 1.0

++++ ito: 9
	ifroms: [4, 6]
	scores: [126.73498602992018, -36.7403289419144]
	Attention weights: [1.00000000e+00 1.00826056e-71]
	sum_i scores_i = 1.0

Summary

From the Attention as a soft dictionary lookup formalism, we can see that Attention’s forward pass is similar to a message passing algorithm. During each step of training, attention tunes the $Q$, $K$, & $V$ projection matrices to achieve more coherent predictions similar to clique calibration in graphical models. In contrast, attention weights do not define joint probability distributions among random variables (like a graphical model), but only distributions over which values should be weighted higher during the forward pass. So while marginal inference is not possible on a trained network with Attention mechanisms, correlations should be preserved from the original nodes.