Relativistic Velocities
A follow up to my earlier posts on time dilation and length contraction. This post will talk about how velocities add under Special Relativity and how it differs that Newton’s laws of motion.
Experimental Setup
As a reminder, Special Relativity is based upon two postulates. One dates back to Galileo and the other has been experimentally verified since the late 1800s.
Postulates of Special Relativity;
- laws of physics are invariant in all inertial frames of reference (principle of relativity).
- all observers see light travel at the same speed, $c$.
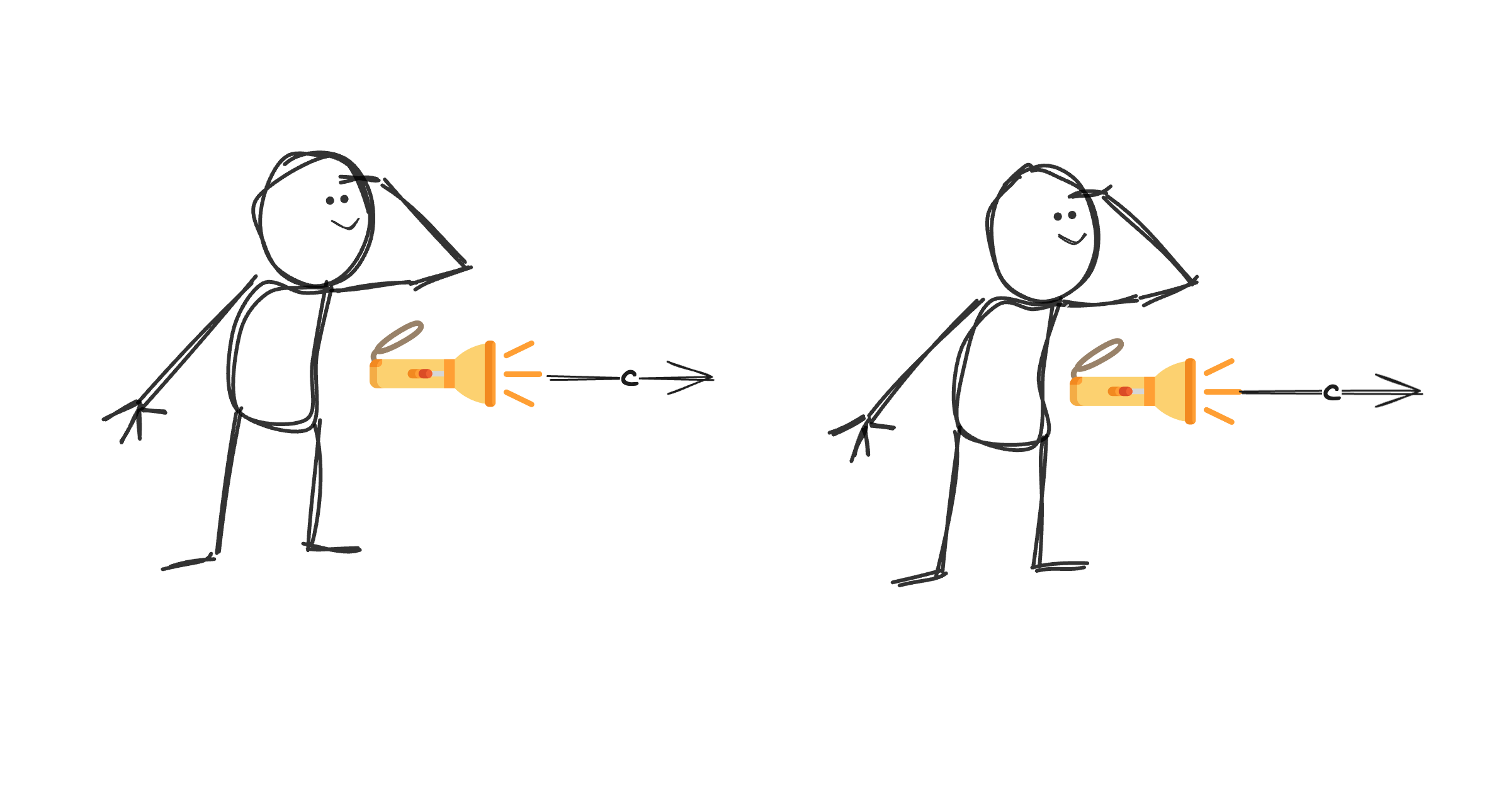
Our experimental setup will involve two people shining flashlights, they are both standing on the same line (we can call this the $x$-axis) and one is positioned before the other. Lets first assume that neither of them are moving relative towards each other (both observers are stationary) to build some intuition about the postulates:
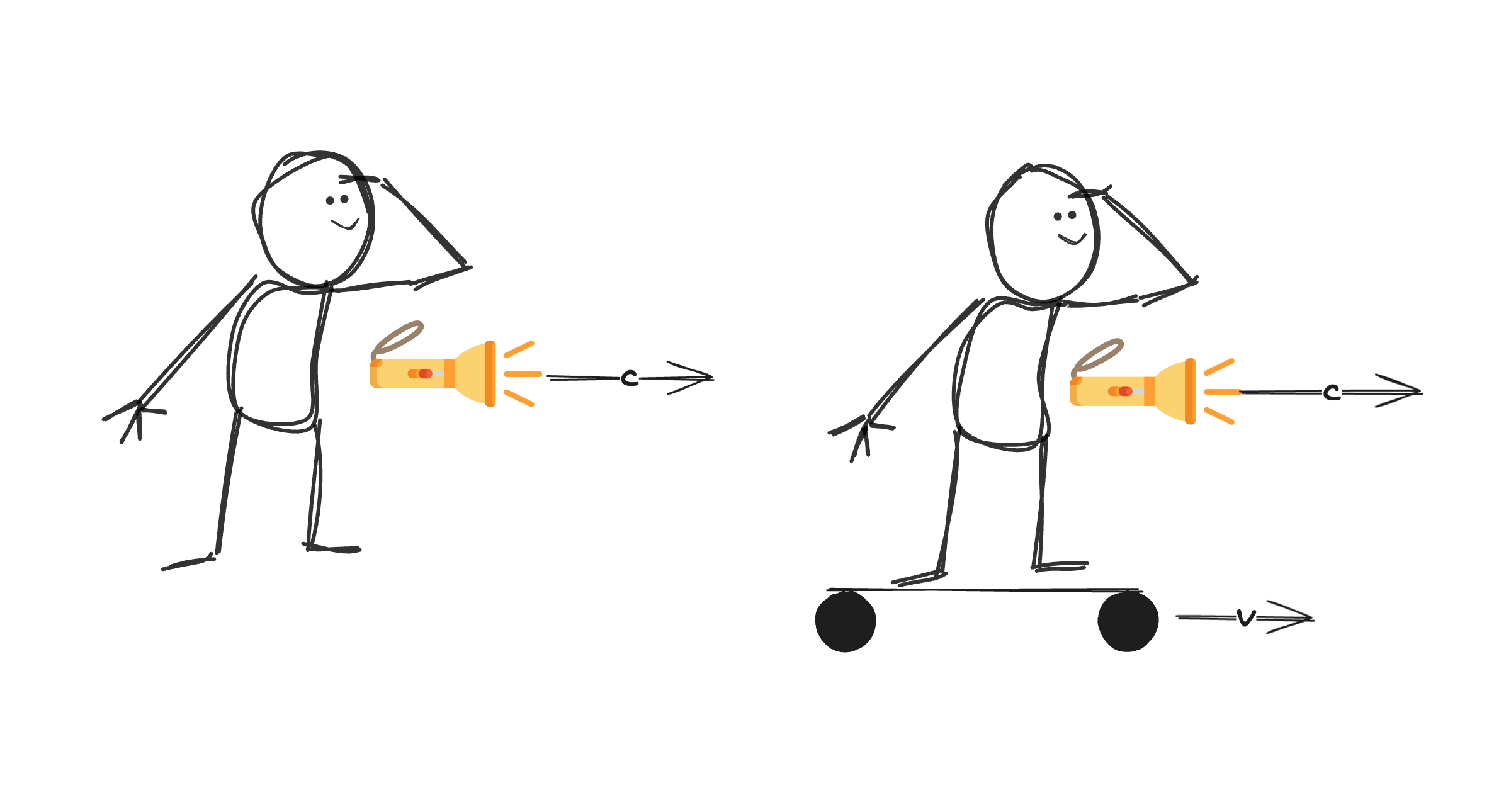
Each observer will see both beams of light moving to the right with speed $c$ (lets assume the observer on the right has some mirror to see the light coming behind them). In this simple case, the postulates of Special Relativity are pretty trivial. Things become more interesting when the observer on the right speeds away from the observer on the left with velocity $v$:
To analyze this more complicated case, we will use two frameworks; Newtonian Mechanics and Relativistic Mechanics (aka Special Relativity).
Newtonian Mechanics
Before Einstein’s paper on Special Relativity in 1905, the calculation would have worked as follows:
Observer on the Left The left observer sees their own beam of light move with speed $c$, no change from before. But for the right beam of light, we need to take into account the frame of reference from where it was emitted (the moving observer on the right). The calculation is simple, the left observer sees the light moving with velocity:
\[v_{\text{right beam}} = v_{\text{right observer}} + c\]If you had trouble with this calculation, just picture a friend throwing a ball from a bike. Intuitively, the ball’s velocity is the velocity of the bike + how fast the ball was thrown.
Despite the simplicity, we have already found a contradiction. Regardless of what frame of reference you are in, all light should be traveling at speed $c$ but we calculated the speed as $v_{\text{right observer}} + c$ which is greater than $c$.
Observer on the Right This calculation is analogous to the above. The right observer sees the rightmost beam move at speed $c$, same as before. They see the left beam travel at speed:
\[v_{\text{left beam}} = -v_{\text{right observer}} + c\]Which runs into a similar contradiction we found above, except now light appears to moving slower than $c$.
Relativistic Mechanics
This contradiction is what Special Relativity was designed to resolve. First, here is the time dilation equation from the earlier post but in a more general form:
\[\begin{align*} t' &= \gamma(t - vx / c^2) \\ x' &= \gamma(x - vt) \end{align*}\]Where $\gamma = \frac{1}{\sqrt{(1 - v^2 / c^2)}}$ as before. This more general form is called the Lorentz Transformation.
To verify the postulates of Special Relativity like we did above, we have to consider a couple extra steps. But first, some notation:
\[\begin{align*} x &= \text{Position of left observer} \\ x' &= \text{Position of right observer} \\ x'' &= \text{Position of right light beam} \\ v &= \text{Velocity of $x'$ relative to $x$} \\ u &= \text{Velocity of $x''$ relative to $x'$} \\ \end{align*}\]Our strategy will be to first compute the Lorentz Transformation of $x’’$ in terms of $x$ & $t$. Then, we will analyze this expression to see how it helps in our experiment with the two flashlight wielding observers.
Compute $x’’$ in terms of $x$ & $t$
Start with $x’’$ expressed in terms of $x’$ using the Lorentz Transformation, then apply another Lorentz Transformation to involve $x$:
\[\begin{align*} x'' &= \frac{1}{\sqrt{1 - u^2 / c^2}}(x' - ut') \\ &= \frac{1}{\sqrt{1 - u^2 / c^2}}(\frac{x - vt}{\sqrt{1 - v^2 / c^2}} - u\frac{t - \frac{vx}{c^2}}{\sqrt{1 - v^2 / c^2}}) \\ &= \frac{1}{\sqrt{1 - u^2 / c^2}}\frac{1}{\sqrt{1 - v^2 / c^2}}(x - vt - ut + \frac{uv x}{c^2}) \\ &= \frac{x - vt - ut + \frac{uv x}{c^2}}{\sqrt{1 - u^2 / c^2}\sqrt{1 - v^2 / c^2}} \end{align*}\]This says that $x’’$’s position is a function of $x$, $v$, and $u$ which intuitively makes sense. If we apply some additional algebra steps, we can actually see that this is itself a Lorentz Transformation in disguise,
\[\begin{align*} \frac{x - vt - ut + \frac{uv x}{c^2}}{\sqrt{1 - u^2 / c^2}\sqrt{1 - v^2 / c^2}} &= \frac{x (1 + \frac{uv}{c^2}) - (u + v)t}{\sqrt{1 - u^2 / c^2}\sqrt{1 - v^2 / c^2}} \\ &= (1 + \frac{uv}{c^2})\frac{x - \frac{u + v}{1 + \frac{uv}{c^2}}t}{\sqrt{1 - u^2 / c^2}\sqrt{1 - v^2 / c^2}} \\ &= \frac{x - \frac{u + v}{1 + \frac{uv}{c^2}}t}{\frac{\sqrt{1 - \frac{u^2}{c^2}}\sqrt{1 - \frac{v^2}{c^2}}}{1 + \frac{uv}{c^2}}} \end{align*}\]Now focusing only on the denominator,
\[\begin{align*} \frac{\sqrt{1 - \frac{u^2}{c^2}}\sqrt{1 - \frac{v^2}{c^2}}}{1 + \frac{uv}{c^2}} &= \frac{\sqrt{1 - \frac{u^2}{c^2} - \frac{v^2}{c^2} + \frac{u^2v^2}{c^4}}}{1 + \frac{uv}{c^2}} \\ &= \sqrt{\frac{1 + \frac{2uv}{c^2} + \frac{u^2v^2}{c^4} - \frac{u^2}{c^2} - \frac{2uv}{c^2} - \frac{v^2}{c^2}}{(1 + \frac{uv}{c^2})^2}} \\ &= \sqrt{\frac{(1 + \frac{uv}{c^2})^2 - \frac{1}{c^2}(u^2 + 2uv + v^2)}{(1 + \frac{uv}{c^2})^2}} \\ &= \sqrt{\frac{c^2(1 + \frac{uv}{c^2})^2 - (u + v)^2}{c^2(1 + \frac{uv}{c^2})^2}} \\ &= \sqrt{1 - \frac{(u + v)^2}{c^2(1 + \frac{uv}{c^2})^2}} \\ &= \sqrt{1 - \frac{(u + v)^2}{c^2(1 + \frac{uv}{c^2})^2}} \\ &= \sqrt{1 - \frac{(\frac{u + v}{1 + \frac{uv}{c^2}})^2}{c^2}} \end{align*}\]And putting it all together:
\[\begin{align*} x'' = \frac{x - \frac{u + v}{1 + \frac{uv}{c^2}}t}{\sqrt{1 - \frac{(\frac{u + v}{1 + \frac{uv}{c^2}})^2}{c^2}}} \end{align*}\]We notice a certain quantity:
\[\begin{align*} w = \frac{u + v}{1 + \frac{uv}{c^2}} \end{align*}\]Which makes $x’’$ look just like a Lorentz Transformation:
\[x'' = \frac{x - wt}{\sqrt{1 - \frac{w^2}{c^2}}}\]But with speed $w$ instead of $v$ or $u$.
A similar argument can find:
\[\begin{align*} t'' = \frac{t - wx / c^2}{\sqrt{1 - w^2}} \end{align*}\]But I think this is already enough algebra!
Analyze $w$ for our experiment
Going back to the experiment, we are now ready to analyze how each observer sees the beams of light. First the simple cases: the left observer still sees the left beam with speed $c$ and the right observer still sees the right beam with speed $c$.
For the left observer viewing the right beam, all we need to do is apply our formula for $w$ since that was derived from $x’’$ in terms of $x$. Setting $u = c$, we see:
\[\begin{align*} w &= \frac{c + v}{1 + \frac{cv}{c^2}} \\ &= \frac{c + v}{\frac{c^2 + cv}{c^2}} \\ &= c^2 \frac{c + v}{c^2 + cv} \\ &= \frac{c^2}{c} \frac{c + v}{c + v} \\ &= c \end{align*}\]The $v’s$ cancel out leaving just $c$! So all observers, regardless of their reference frame, always see light traveling at $c$ thus avoiding the contradiction.
But certainly this must be a fluke! What if we went crazy and said that $v = u = c$ that the right observer was traveling at light speed and then shot a light beam from their flashlight? In this case:
\[\begin{align*} w &= \frac{c + c}{1 + \frac{c^2}{c^2}} \\ &= \frac{2c}{2} \\ &= c \end{align*}\]The left observer would still see the right beam traveling at $c$!
Conclusion
We found a contradiction concerning light when using additive velocity vectors of Newtonian Mechanics. Instead, using Relativistic Mechanics, we can avoid this contradiction using the Lorentz Transformation. Indeed, the Lorentz Transformation is derived with this property in mind and necessarily keeps the speed of light at $c$ by adjusting $x’$ and $t’$ instead.