Monte Carlo Tree Search LLM

A post on how to combine an LLM with the Monte Carlo Tree Search (MCTS) algorithm. There are numerous versions of MCTS, I follow Planning with Large Language Models for Code Generation’s implementation with the following additions:

• Allow step-level expansions instead of just token-level (for more discussion on token vs. step level, see section 3 of this paper).
• Pass generic callable’s for the candidate generation, simulation, and reward.

Code is available here which is heavily inspired from this excellent blog post.

MCTS

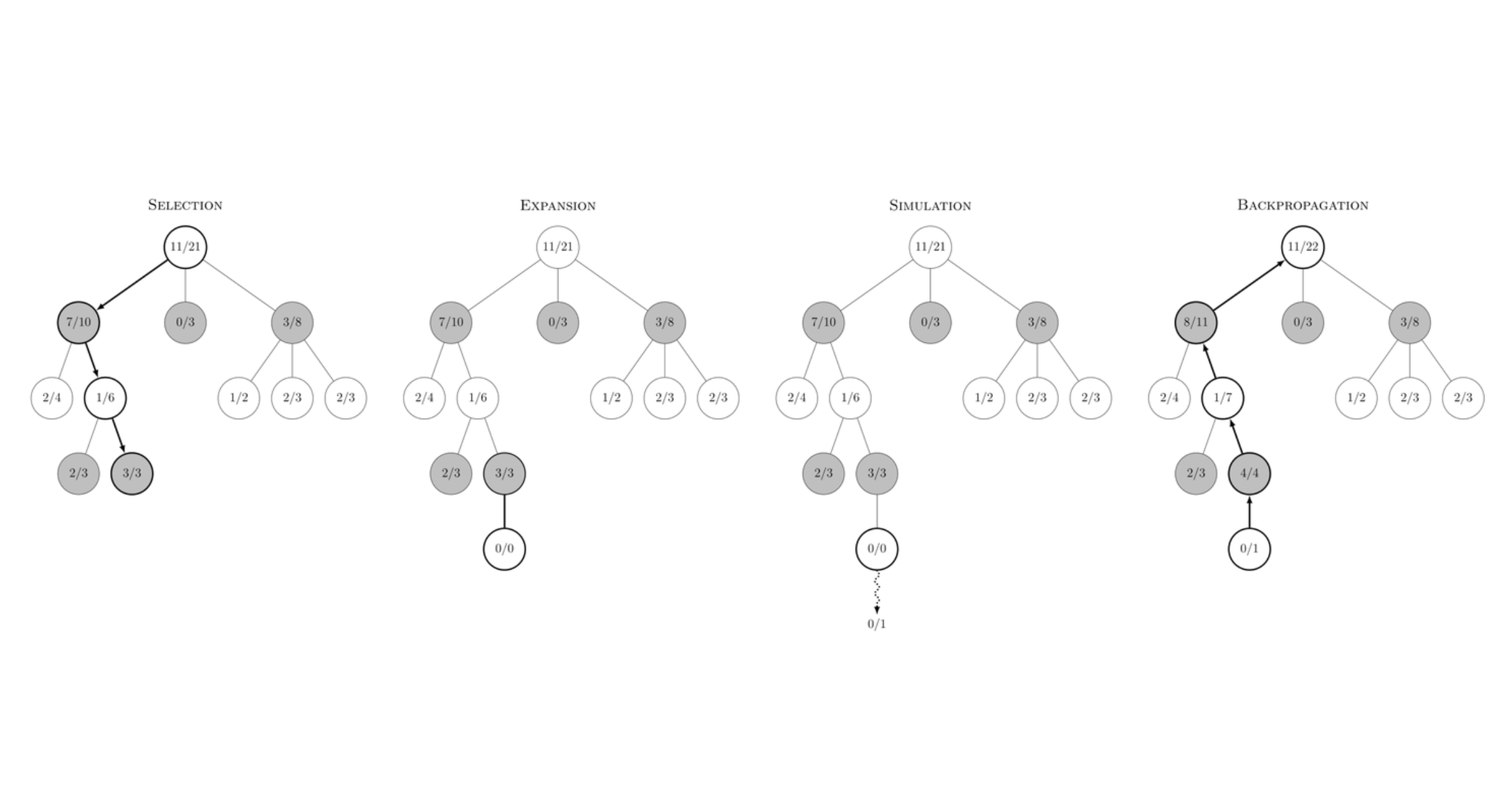
First, I outline appendix D.1 PG-TD from Planning with Large Language Models for Code Generation which covers the adapted MCTS algorithm.

Select

• Starting from the root node (initialized as an empty string: “” or a prompt: “The dog ran”), recursively select subtrees until finding a node that has not previously been expanded.
• Each node maintains a cache $Q(s, a)$ which is the maximum reward (could also be the average reward) obtained by starting from a state $s$ and taking action $a$.

Code Snippet

• Selection is defined as:

\[\text{P_UCB_SELECT}(s, c) = \arg \max_a \text{P-UCB}(s, a)\]

Using the selection criterion $\text{P-UCB}$ defined as:

\[\text{P-UCB}(s, a) = Q(s, a) + \beta(s) \cdot P_{\text{transformer}}(a | s) \cdot \frac{\sqrt{\log{s.visits}}}{1 + s'.visits}\]

where $s$ is the parent state, $s’$ is the new state after taking action $a$ from $s$, and $\beta(s)$ is computed as:

\[\beta(s) = \log{\frac{s.visits + c_{\text{base}} + 1}{c_{\text{base}}}} + c\]

And finally $c$ is a constant that encourages exploration.

Code Snippet

Expansion

• Once at the selected node, add children to this node with a set of candidate actions.
• The top-k candidate actions are taken from the conditional distribution produced by the transformer:

\[\{a\}_{i=1}^k = \max_{1:k} P_{\text{transformer}}(a | s)\]

• In the case of token-level MCTS, we only sample the top-k tokens conditioned on the selected node’s state.
• For step-level MCTS, we can sample an entire path (multiple steps of tokens), recording the top-k candidates at each step. For example, we may sample:

Parent node's state: The dog ran
===
Expansion token 1: {very, extremely, slightly}
Expansion token 2 | very: {fast, slow, randomly}
===
1st candidate node's state: The dog ran very
2nd candidate node's state: The dog ran extremely
3rd candidate node's state: The dog ran slightly
4th candidate node's state: The dog ran very fast
5th candidate node's state: The dog ran very slow
6th candidate node's state: The dog ran very randomly

This may vary depending on the LLM’s generation API, but the above is compatible for any model returning the top-k candidate tokens at each generation step.

Code Snippet

Evaluation

• Conduct a beam search starting from the selected node. This has the effect of a “simulation” where we try to complete the program, translation, or statement from the current node.

Evaluation is done on the current selected node, not the candidate nodes created in the expansion step. Beam search is used loosely as the beam width is set to 1 (also known as hill climbing).

• Compute a reward using the completed evaluation. This can either be a deterministic scoring (compiler passes, math proof is correct) or a score from an LLM judge.

Code Snippet

Backpropagation

• Computed reward is backpropagated recursively back to the root node using the update:

\[Q(\tilde s, \tilde a) \leftarrow \max(Q(\tilde s, \tilde a), r)\]

Each iteration leaves the algorithm in the state where $Q(\tilde s, \tilde a)$ represents the best possible reward achievable from state $s$ taking action $a$.

Code Snippet

One Step of MCTS

Putting it all together, we arrive at one step of MCTS:

Code Snippet

Translation Example

In this demo notebook, I show how MCTS can be used to improve translation from Chinese text to English:

Jupyter Notebook

Conclusion

MCTS is a tree search algorithm that is capable of searching large action spaces. It uses a select-expand-simulate-backpropagate pattern which is highly customizable for different use cases. As LLM performance improves with time, MCTS can always be used at inference time to build a diverse set of generations that mimic human reasoning.