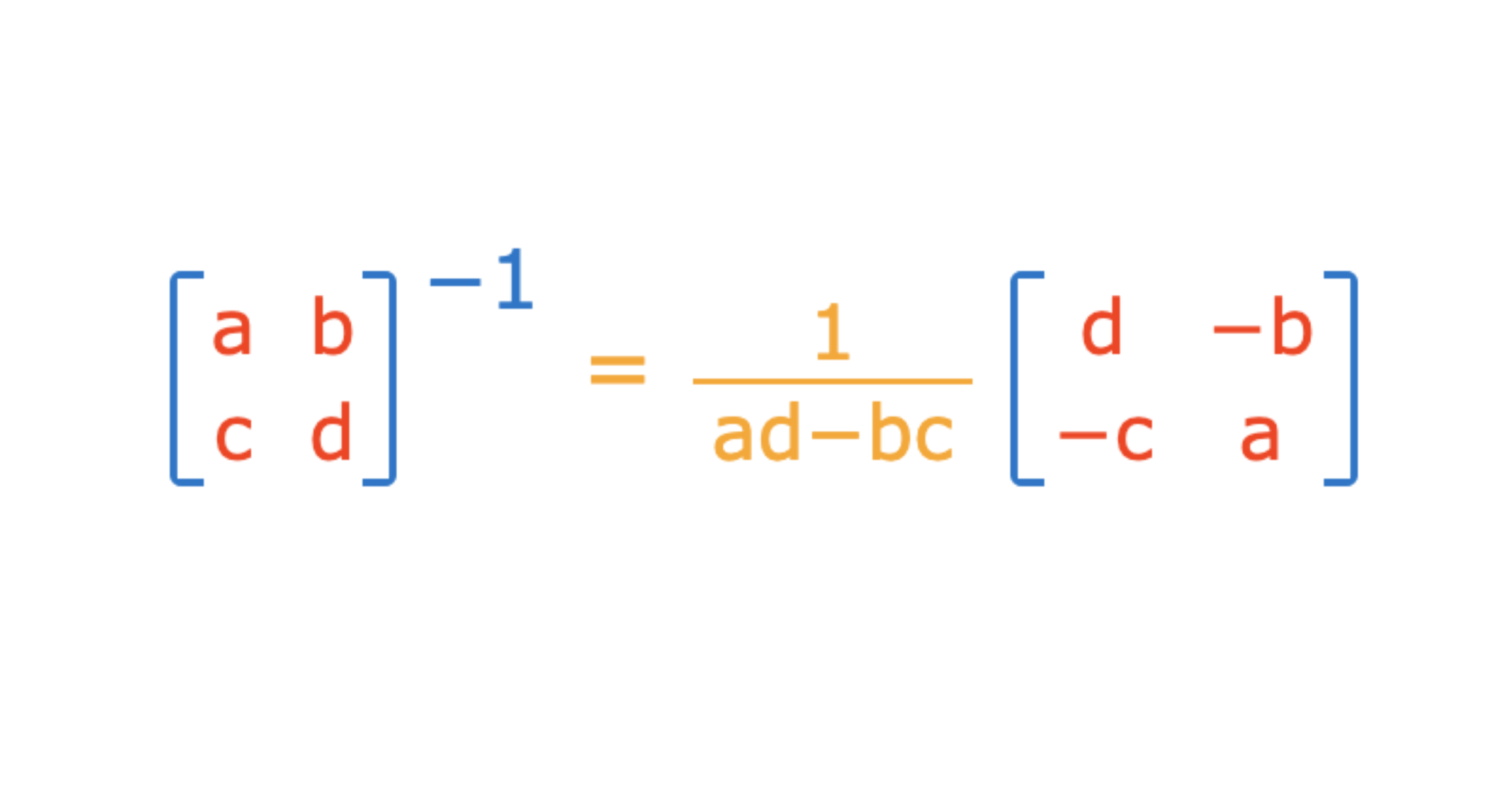Matrix Inverses in PyTorch

A post covering how to complete matrix inversions in PyTorch using BLAS and LAPACK operations. This is particularly useful in Statistics for inverting covariance matrices to form statistical estimators. I came across this recently during a code review and wanted to collect my thoughts on the topic.

Matrix Inverse

First, I review how to compute a matrix-inverse product exactly the way they are presented in statistical textbooks.

\[\begin{align*} Ax &= b \\ x &= A^{-1}b \\ \end{align*}\]

Where $A \in \mathbb R ^{n \times n}$ is a positive semi-definite (PSD) matrix:

\[\begin{align*} x^T A x &\geq 0 \end{align*}\]

For all non-zero $x \in \mathbb R^n$. We can solve this in PyTorch by using torch.linalg.inv:

import torch

# Set the seed for reproducibility
torch.manual_seed(1)
# Use double precision
torch.set_default_dtype(torch.float64)

a = torch.randn(3, 3)
b = torch.randn(3, 2)
# Create a PSD matrix
A = a @ a.T + torch.eye(3) * 1e-3
x = torch.linalg.inv(A) @ b
x_original = x
x

tensor([[-3.2998, -3.1372],
        [-0.6995, -0.0583],
        [-1.3701, -0.7586]])

The problem with this is that it can become numerically instable for poorly conditioned matrices.

In general, we want to use matrix decompositions and avoid inverting matrices as shown in this blog post.

Cholesky Decomposition

We can avoid a matrix inverse by considering the cholesky decomposition of $A$ (giving us a lower triangular matrix $L$):

\[\begin{align*} A &= LL^T \\ LL^T x &= b \\ L^T x &= c \\ Lc &= b \end{align*}\] \[\begin{align*} \text{Forward solve } Lc &= b \text{ for $c$} \\ \text{Backwards solve } L^Tx &= c \text{ for $x$} \\ \end{align*}\]

Which can be solved efficiently using forwards-backwards substitution. In PyTorch, we can use torch.cholesky and torch.cholesky_solve:

L = torch.linalg.cholesky(A)
x = torch.cholesky_solve(b, L)
x

tensor([[-3.2998, -3.1372],
        [-0.6995, -0.0583],
        [-1.3701, -0.7586]])

torch.dist(x, x_original)

tensor(2.6879e-15)

Importantly, this can be accomplished through matrix multiplication and forwards-backwards algorithm without taking any matrix inverse (see this comment for a description).

LU Decomposition

We can also do this with a LU decomposition where $L$ is a lower triangular matrix and $U$ is an upper triangular matrix:

\[\begin{align*} A &= LU \\ LU x &= b \\ \text{Set } U x &= c \\ Lc &= b \end{align*}\] \[\begin{align*} \text{Forward solve } Lc &= b \text{ for $c$} \\ \text{Backwards solve } Ux &= c \text{ for $x$} \\ \end{align*}\]

In PyTorch, we can use torch.linalg.lu_factor and torch.linalg.lu_solve:

LU, pivots = torch.linalg.lu_factor(A)
x = torch.linalg.lu_solve(LU, pivots, b)
x

tensor([[-3.2998, -3.1372],
        [-0.6995, -0.0583],
        [-1.3701, -0.7586]])

torch.dist(x, x_original)

tensor(8.5664e-16)

LDL Decomposition

The same applies to an LDL decomposition which is very similar to the cholesky decomposition. LDL decomposition includes an extra diagonal matrix $D$ but avoids computing the square root of the matrix:

\[\begin{align*} A &= LDL \\ LDL x &= b \\ \text{Set } Lx &= c \\ \text{Set } Dc &= d \\ Ld &= b \end{align*}\] \[\begin{align*} \text{Forward solve } Ld &= b \text{ for $d$} \\ \text{Compute } c &= D^{-1}d \\ \text{Forward solve } Lx &= c \text{ for $x$} \\ \end{align*}\]

Note, we do take $D^{-1}$, but since this is a diagonal matrix, the inverse can be computed analytically by simply inverting each diagonal entry.

In PyTorch, we can use (the experimental) torch.linalg.ldl_factor and torch.linalg.ldl_solve:

LD, pivots = torch.linalg.ldl_factor(A)
x = torch.linalg.ldl_solve(LD, pivots, b)
x

tensor([[-3.2998, -3.1372],
        [-0.6995, -0.0583],
        [-1.3701, -0.7586]])

torch.dist(x, x_original)

tensor(6.8664e-16)

QR Decomposition

We can also use the QR decomposition where $Q$ is an orthogonal matrix and $R$ is upper right triangular matrix:

\[\begin{align*} A &= QR \\ QR x &= b \\ \text{Set } R x &= c \\ Qc &= b \\ c &= Q^T b \end{align*}\] \[\begin{align*} \text{Backwards solve } Rx &= c \text{ for $x$} \\ \end{align*}\]

In PyTorch, we can use torch.linalg.qr and torch.linalg.solve_triangular:

Q, R = torch.linalg.qr(A)
c = Q.T @ b
x = torch.linalg.solve_triangular(R, c, upper=True)
x

tensor([[-3.2998, -3.1372],
        [-0.6995, -0.0583],
        [-1.3701, -0.7586]])

torch.dist(x, x_original)

tensor(2.1020e-15)

SVD

We can also use the singular value decomposition where $U$ is an orthogonal matrix, $S$ is a diagonal matrix, and $V$ is a orthogonal matrix (in the special case that $A$ is a real square matrix):

\[\begin{align*} A &= USV^T \\ USV^Tx &= b \\ x &= (VS^{-1}U^T)b \end{align*}\]

Note, we do take $S^{-1}$, but since this is a diagonal matrix, the inverse can be computed analytically by simply inverting each diagonal entry.

In PyTorch, we can use torch.linalg.svd:

U, S, Vh = torch.linalg.svd(A, full_matrices=False)
x = Vh.T @ torch.diag(1 / S) @ U.T @ b
x

tensor([[-3.2998, -3.1372],
        [-0.6995, -0.0583],
        [-1.3701, -0.7586]])

torch.dist(x, x_original)

tensor(1.6614e-14)

Summary

Here is a summary table of these different options:

Method	Applicable Matrices	Computational Complexity	Efficiency	Stability	Additional Benefits
Cholesky	Symmetric positive def.	$O(n³/3)$	Highest for applicable	Very good	Memory efficient
LU	Square	$O(2n³/3)$	Good for general cases	Good w/ pivot	Useful for determinants and inverses
LDL	Symmetric	$O(n³/3)$	Good for symmetric	Good	Avoids square roots
QR	Any	$O(2mn² - 2n³/3)$ for $m≥n$	Less than LU for square	Very good	Best for least squares
SVD	Any	$O(\min(mn², m²n))$	Lowest	Excellent	Best for ill-conditioned systems

Blackbox Matrix-Matrix Multiplication (BBMM)

Since matrix inversion is especially relevant to Gaussian Processes, the library GPyTorch has implemented a Blackbox Matrix-Matrix Gaussian Process Inference with GPU Acceleration library. Importantly, it lowers the cost of the above approaches from $O(n^3)$ to $O(n^2)$ and allows routines to be used on GPU architectures. GPyTorch uses LinearOperator which is useful for exploiting specific matrix structure:

from linear_operator.operators import DiagLinearOperator, LowRankRootLinearOperator
C = torch.randn(1000, 20)
d = torch.ones(1000) * 1e-9
b = torch.randn(1000)
A = LowRankRootLinearOperator(C) + DiagLinearOperator(d)
_ = torch.linalg.solve(A, b)