Markov Social Inequality

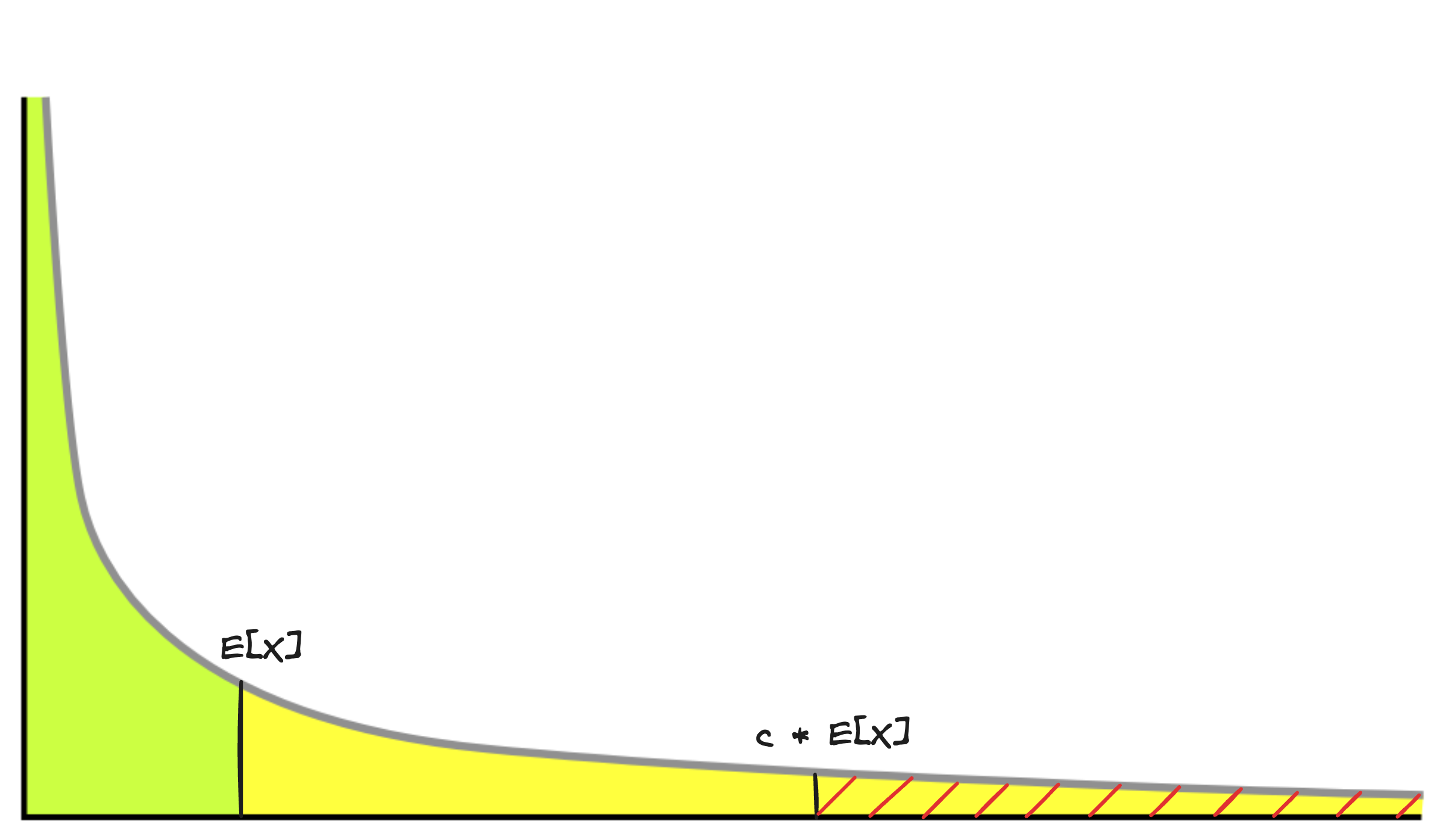
Consider a nonnegative random variable $X$ (i.e. annual income, home value, stock price). Here is the famous Markov Inequality ¹:

\[\begin{flalign} \mathbb E [X] &= \int_{-\infty}^{\infty} x f(x) dx \\ &= \int_{0}^{\infty} x f(x) dx \\ &\geq \int_{a}^{\infty} x f(x) dx \\ &\geq \int_{a}^{\infty} a f(x) dx \\ &= a \int_{a}^{\infty} f(x) dx \\ & = a P(X \geq a) \\ &\therefore P(X \geq a) \leq \frac{\mathbb E[X]}{a} \end{flalign}\]

Now set $a = c \cdot \mathbb E[X]$,

\[\begin{flalign} P(X \geq c \cdot \mathbb E[X]) \leq \frac{\mathbb E[X]}{c \cdot \mathbb E[X]} \\ \therefore P(X \geq c \cdot \mathbb E[X]) \leq \frac{1}{c} \end{flalign}\]

For example, $c=10$ says that the probability of $X$ being 10 times it’s average is at most $\frac{1}{10}$.

In 2023, the estimated average GDP per capita (PPP) over all countries was $23,452$ ². This means that at most $\frac{1}{4.26} \approx 23.4\%$ of countries can have more than $100,000$ GDP per capita. Only 5 out of the 178 had GDP per capita in 2023, showing how conservative this bound can be.

1. https://en.wikipedia.org/wiki/Markov%27s_inequality ↩︎

2. https://en.wikipedia.org/wiki/List_of_countries_by_GDP_(PPP)_per_capita ↩︎