Ising Model (Computation, pt. 2)
Ising Model (Computation, pt. 2)
A post about the computation of the Ising Model.
Ising Model Code
Code inspired by this post by @Jake VanderPlas which compares Python against cPython.
1
2
3
4
5
6
7
8
import numpy as np
import pandas as pd
import plotly.express as px
import plotly.graph_objects as go
from IPython.display import display, Markdown
from typing import List
np.random.seed(1)
MCMC Implementations
Below I copy+pasted the functions directly from @Jake VanderPlas blog post. Looking back to the update equations for MH, MCMC:
\[A(x' | x) = \min{\big[ 1, \exp{-2\beta x_n \sum_m J_{n,m} x_m + h} \big ]}\]We recognize the original blog post’s update as a MH, MCMC step.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# Functions from Jake VanderPlas's blog post.
def random_spin_field(N, M):
return np.random.choice([-1, 1], size=(N, M))
# Add an `update_fn` arg.
def ising_step(field, update_fn, beta=0.4):
N, M = field.shape
for n_offset in range(2):
for m_offset in range(2):
for n in range(n_offset, N, 2):
for m in range(m_offset, M, 2):
update_fn(field, n, m, beta)
return field
def _ising_update(field, n, m, beta):
total = 0
N, M = field.shape
for i in range(n - 1, n + 2):
for j in range(m - 1, m + 2):
if i == n and j == m:
continue
total += field[i % N, j % M]
dE = 2 * field[n, m] * total
if dE <= 0:
field[n, m] *= -1
elif np.exp(-dE * beta) > np.random.rand():
field[n, m] *= -1
We can also add in the Gibbs Sampling step:
\[P(x_n = 1 | \{x_i\}_{i \neq n}) = \sigma(2\beta\sum_{m}J_{n, m}x_m + h)\]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# Also make a random stepping Ising update.
def sigmoid(x: float) -> float:
# 700 seems to be the magic number where numpy will overflow.
# In this case, analytically handle the probability
if -x > 700:
return 0.0
return float(1 / (1 + np.exp(-x)))
def _ising_update_gibbs(field: np.ndarray, n: int, m: int, beta: float) -> None:
total = 0
N, M = field.shape
for i in range(n - 1, n + 2):
for j in range(m - 1, m + 2):
if i == n and j == m:
continue
total += field[i % N, j % M]
dE = 2 * beta * total
if sigmoid(dE) > np.random.rand():
field[n, m] = 1
else:
field[n, m] = -1
Plotting Helpers
A couple helper functions so that we can plot to markdown.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
# Plotting helper functions.
def render_plotly_html(fig: go.Figure) -> None:
"""Display a Plotly figure in markdown with HTML."""
# Ensure frame is square
display(
Markdown(
fig.to_html(
include_plotlyjs="cdn",
)
)
)
def _grid_to_long(grid: np.ndarray) -> np.ndarray:
"""Convert a N x M matrix into a (N x M, 2) long vector."""
# x coordinate, y coordinate, spin of the coordinate.
return np.vstack(
[*map(lambda x: x.flatten(), np.indices(grid.shape)), grid.flatten()]
).T
def grids_to_long(grids: List[np.ndarray]) -> pd.DataFrame:
"""Convert a n-list of grid matrices into a long-format DataFrame.
Args:
grids: List of grid matrices ordered by time.
Returns:
DataFrame with each N x M matrix converted to a (N x M, 2) section.
Each section is indexed by the order in `grids`.
"""
t = np.array([[i] * np.prod(grid.shape) for i, grid in enumerate(grids)])
df = pd.DataFrame(np.concatenate([_grid_to_long(i) for i in grids]))
df["t"] = t.flatten()
df.columns = ["x", "y", "spin", "t"]
return df
Sampling
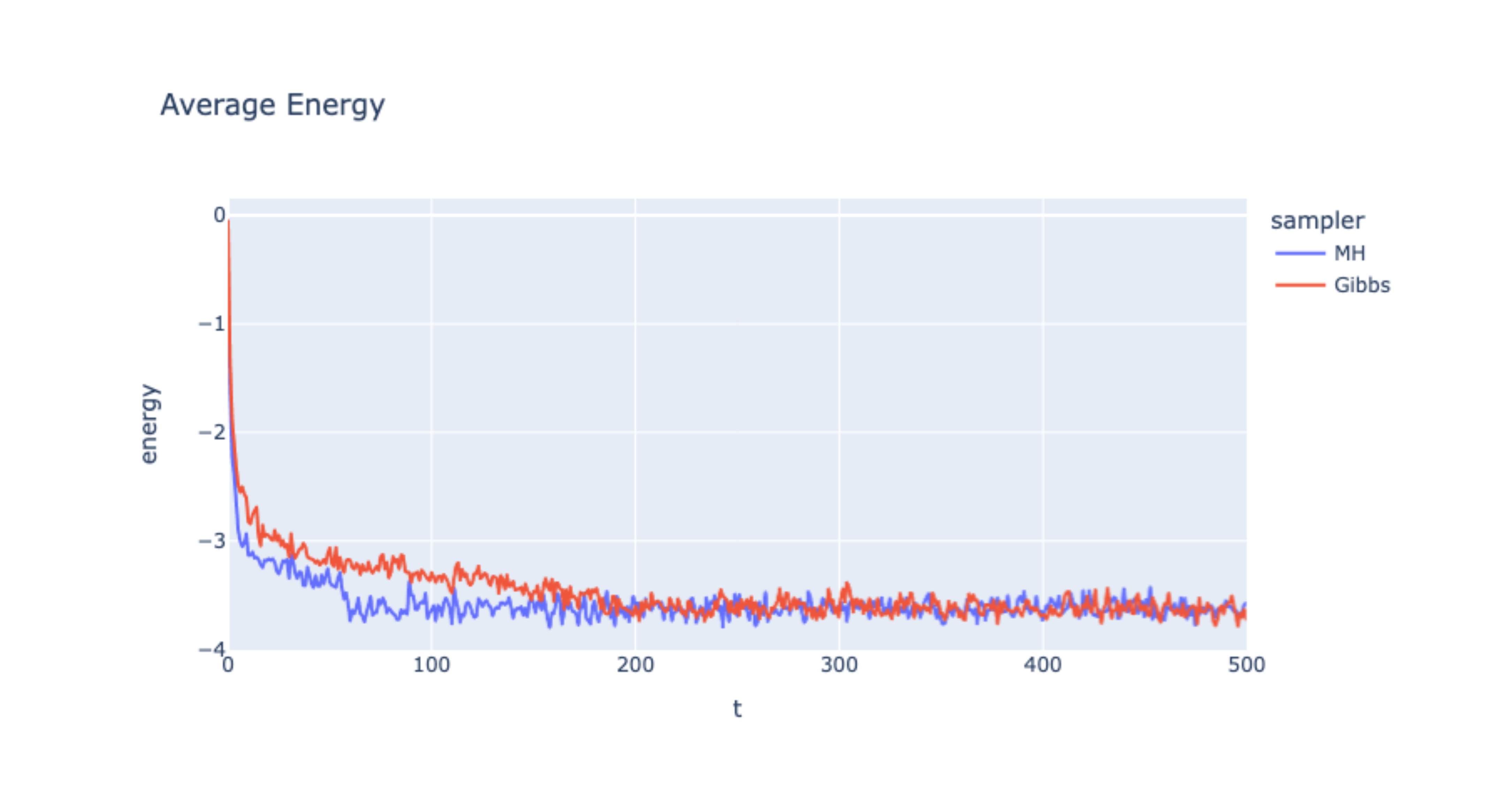
Now we can sample both MH MCMC and Gibbs Sampling and compare the results.
1
2
3
4
5
N, M = 40, 40
STEPS = 500
BETA = 0.25
# Start from the same random initial configuration.
images = [random_spin_field(N, M)]
1
2
3
4
5
mh_images = images.copy()
for i in range(STEPS):
mh_images.append(ising_step(mh_images[-1].copy(), beta=BETA, update_fn=_ising_update))
mh_steps = grids_to_long(mh_images)
mh_steps["sampler"] = "MH"
1
2
3
4
5
gibbs_images = images.copy()
for i in range(STEPS):
gibbs_images.append(ising_step(gibbs_images[-1].copy(), beta=BETA, update_fn=_ising_update_gibbs))
gibbs_steps = grids_to_long(gibbs_images)
gibbs_steps["sampler"] = "Gibbs"
Plots
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
# Plot the simulation as a time lapse in Plotly.
fig = px.scatter(
mh_steps,
x="x",
y="y",
color="spin",
color_continuous_scale="thermal",
animation_frame="t",
hover_name="t",
)
fig.update(layout_coloraxis_showscale=False)
# Ensure frame is square
fig.update_yaxes(
scaleanchor="x",
scaleratio=1,
)
render_plotly_html(fig)